Turunan Fungsi Trigonometri
Rumus dasar turunan fungsi trigonometri adalah turunan fungsi sinus dan kosinus, yang diperoleh dari konsep limit, yakni sebagai berikut:
Jika y = sin x maka y� = cos x
Jika y = cos x maka y� = �sin x
Dari rumus dasar tersebut, diturunkanlah rumus pengembangan, yakni turunan fungsi tangens, cotangens, secan dan cosecan. Proses pengembangan rumus tersebut adalah
Jika y = tan x maka y� = sec2x
Jika y = cot x maka y� = � cosec2x
Jika y = sec x maka y� = sec x . tan x
Jika y = cosec x maka y� = � cosec x . tan x
Selanjutnya, terdapat rumus pengembangan turunan fungsi trigonometri dengan aturan rantai, yakni sebagai berikut :
Misalkan u(x) adalah fungsi yang terdefinisi pada x bilangan real dan f(u) = sin u, maka untuk y = f [u(x)] diperoleh y� = f � [u(x)]. u�(x)
y� = (cos u)(u�)
y� = u�.cos u
Sehingga dengan cara yang sama dapat disimpulkan bahwa jika u adalah fungsi yang terdefinisi pada bilangan real, maka diperoleh:
Untuk y = sin u maka y� = u�.cos u
Untuk y = cos u maka y� = �u�.sin u
Untuk y = tan u maka y� = u�. sec2u
Untuk y = cot u maka y� = u'. cosec2u
Untuk y = sec u maka y� = u�. sec u . tan u
Untuk y = csc u maka y� = �u�. cosec u . tan u
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
01. Tentukanlah turunan pertama dari setiap fungsi berikut ini :
(a) f(x) = cos (3x � 4)
(b) f(x) = 3.tan (x2 � 4)
(c) f(x) = cot (2x + 5) � 5.sec(x2 � 4)
(d) f(x) = 4x2 � sec(2x2 + 3x)
Jawab
(a) f(x) = cos (3x � 4)
Maka
f �(x) = (3)(�sin(3x � 4))
f �(x) = �3.sin(3x � 4)
(b) f(x) = 3.tan (x2 � 4)
Maka
f �(x) = (2x)(3)sec2 (x2 � 4)
f �(x) = 2x sec2 (x2 � 4)
(c) f(x) = cot (2x + 5) � 5 . sec(x2 � 4)
Maka
f �(x) = (2)(5)(2 . sec2x) � (2x)(5.sec(x2 � 4).tan(x2 � 4))
f �(x) = 20 . sec2x � 10x.sec(x2 � 4).tan(x2 � 4)
(d) f(x) = 4x2 � sec(2x2 + 3x)
Maka f �(x) = 8x � ((4x + 3) sec(x2 + 3x).tan(2x2 + 3x))
02. Tentukanlah turunan pertama dari setiap fungsi berikut ini:


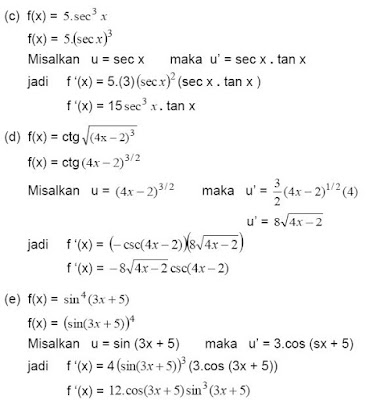
03. Tentukanlah turunan pertama dari setiap fungsi berikut ini:

jawab


04. Tentukanlah nilai setiap turunan berikut ini untuk x bilangan real yang diberikan:

jawab


Jika y = sin x maka y� = cos x
Jika y = cos x maka y� = �sin x
Dari rumus dasar tersebut, diturunkanlah rumus pengembangan, yakni turunan fungsi tangens, cotangens, secan dan cosecan. Proses pengembangan rumus tersebut adalah
Jika y = tan x maka y� = sec2x
Jika y = cot x maka y� = � cosec2x
Jika y = sec x maka y� = sec x . tan x
Jika y = cosec x maka y� = � cosec x . tan x
Selanjutnya, terdapat rumus pengembangan turunan fungsi trigonometri dengan aturan rantai, yakni sebagai berikut :
Misalkan u(x) adalah fungsi yang terdefinisi pada x bilangan real dan f(u) = sin u, maka untuk y = f [u(x)] diperoleh y� = f � [u(x)]. u�(x)
y� = (cos u)(u�)
y� = u�.cos u
Sehingga dengan cara yang sama dapat disimpulkan bahwa jika u adalah fungsi yang terdefinisi pada bilangan real, maka diperoleh:
Untuk y = sin u maka y� = u�.cos u
Untuk y = cos u maka y� = �u�.sin u
Untuk y = tan u maka y� = u�. sec2u
Untuk y = cot u maka y� = u'. cosec2u
Untuk y = sec u maka y� = u�. sec u . tan u
Untuk y = csc u maka y� = �u�. cosec u . tan u
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
01. Tentukanlah turunan pertama dari setiap fungsi berikut ini :
(a) f(x) = cos (3x � 4)
(b) f(x) = 3.tan (x2 � 4)
(c) f(x) = cot (2x + 5) � 5.sec(x2 � 4)
(d) f(x) = 4x2 � sec(2x2 + 3x)
Jawab
(a) f(x) = cos (3x � 4)
Maka
f �(x) = (3)(�sin(3x � 4))
f �(x) = �3.sin(3x � 4)
(b) f(x) = 3.tan (x2 � 4)
Maka
f �(x) = (2x)(3)sec2 (x2 � 4)
f �(x) = 2x sec2 (x2 � 4)
(c) f(x) = cot (2x + 5) � 5 . sec(x2 � 4)
Maka
f �(x) = (2)(5)(2 . sec2x) � (2x)(5.sec(x2 � 4).tan(x2 � 4))
f �(x) = 20 . sec2x � 10x.sec(x2 � 4).tan(x2 � 4)
(d) f(x) = 4x2 � sec(2x2 + 3x)
Maka f �(x) = 8x � ((4x + 3) sec(x2 + 3x).tan(2x2 + 3x))
02. Tentukanlah turunan pertama dari setiap fungsi berikut ini:


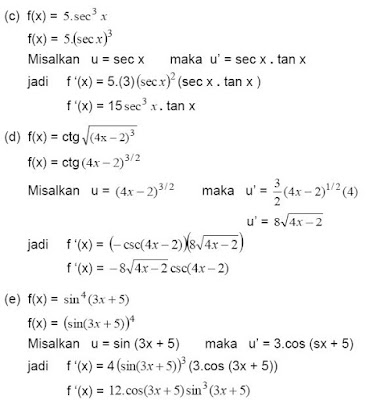
03. Tentukanlah turunan pertama dari setiap fungsi berikut ini:

jawab


04. Tentukanlah nilai setiap turunan berikut ini untuk x bilangan real yang diberikan:

jawab


