Melukis Grafik Fungsi Polinom

Langkah- Langkah melukis Grafik Fungsi polinom
1. Menentukan titik potong dengan sumbu X dan sumbu Y (jika mudah ditentukan)
2. Menentukan interval fungsi naik dan fungsi turun serta titik-titik stasionernya
3. Menentukan Interval cekung atas dan cekung bawah fungsi serta titik beloknya
4. Melukis sketsa grafik

Untuk lebih jelasnya, ikutilah contoh soal berikut ini :
01. Lukislah grafik fungsi polinom f(x) = x³ � 9x² + 24x � 10
Jawab
Langkah 1 : Menentukan titik potong dengan sumbu-sumbu koordinat.
Titik potong dengan sumbu-x sulit ditentukan
Titik potong dengan sumbu-y
Syarat : x = 0
Maka :
y = (0)³ � 9(0)² + 24(0) � 10
y = �10
Titiknya (0, �10)
Langkah 2 : Interval fungsi naik dan turun
f(x) = x³ � 9x² + 24x � 10
f�(x) = 3x² � 18x + 24
maka:
f�(x) = 0
3x² � 18x + 24 = 0
x² � 16x + 8 = 0
(x � 4)(x � 2) = 0
x1 = 2 dan x2 = 4

Uji : x = 0 maka f�(0) = 3(0)² � 18(0) + 24 = 24 > 0 (fungsi naik)
Uji : x = 3 maka f�(3) = 3(3)² � 18(3) + 24 = �3 < 0 (fungsi turun)
Uji : x = 5 maka f�(4) = 3(5)² � 18(5) + 24 = 9 > 0 (fungsi naik)

Sehingga interval fungsi naik pada x < 2 atau x > 4
interval fungsi turun pada 2 < x < 4
Titik stasionernya :
x = 2 maka f(2) = (2)³ � 9(2)² + 24(2) � 10 = 10 , Titik maksimum di (2, 10)
x = 4 maka f(4) = (4)³ � 9(4)² + 24(4) � 10 = �5 , Titik minimum di (4, �42)
Langkah 3 : Menentukan interval cekung atas dan cekung bawah
f(x) = x³ � 9x² + 24x � 10
f�(x) = 3x² � 18x + 24
f��(x) = 6x � 18
maka f��(x) = 0
6x � 18 = 0
6x = 18 maka x = 3

Uji : x = 0 maka f��(0) = 6(0) � 18 = �18 < 0 (cekung bawah)
Uji : x = 4 maka f��(4) = 6(4) � 18 = 6 > 0 (cekung atas)
Koordinat titik beloknya :
x = 3 maka f(3) = (3)³ � 9(3)² + 24(3) � 10 = 29 Jadi titiknya (3, 8)
Gambar grafiknya:


02. Lukislah grafik fungsi polinom f(x) = x³ + 3x² � 9x � 20
Jawab
Langkah 1 : Menentukan titik potong dengan sumbu-sumbu koordinat.
Titik potong dengan sumbu-x sulit ditentukan
Titik potong dengan sumbu-y
Syarat : x = 0
Maka :
y = (0)³ + 3(0)² � 9(0) � 20
y = �20
Titiknya (0, �20)
Langkah 2 : Interval fungsi naik dan turun
f(x) = x² + 3x² � 9x � 20
f�(x) = 3x² + 6x � 9
maka:
f�(x) = 0
3x² + 6x � 9 = 0
x² + 2x � 3 = 0
(x + 3)(x � 1) = 0
x1 = �3 dan x2 = 1

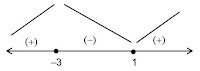
Uji : x = �4 maka f�(�4) = 3(�4)² + 6(�4) � 9 = 15 > 0 (fungsi naik)
Uji : x = 0 maka f�(3) = 3(0)² + 6(0) � 9 = �9 < 0 (fungsi turun)
Uji : x = 2 maka f�(2) = 3(2)² + 6(2) � 9 = 15 > 0 (fungsi naik)
Sehingga interval fungsi naik pada x < �3 atau x > 1
interval fungsi turun pada �3 < x < 1
Titik stasionernya :
x = �3 maka f(�3) = (�3)³ + 3(�3)² � 9(�3) � 20 = 7 , Titik maksimum di (�3, 7)
x = 1 maka f(1) = (1)³ + 3(1)² � 9(1) � 20 = �25 , Titik minimum di (1, �25)
Langkah 3 : Menentukan interval cekung atas dan cekung bawah
f(x) = x³ + 3x² � 9x � 20
f�(x) = f�(x) = 3x² + 6x � 9
f��(x) = 6x + 6
maka
f��(x) = 0
6x + 6 = 0
6x = �6
x = �1

Uji : x = �2 maka f��(�2) = 6(�2) + 6 = �6 < 0 (cekung bawah)
Uji : x = 0 maka f��(0) = 6(0) + 6 = 6 > 0 (cekung atas)
Koordinat titik beloknya :
x = �1 maka f(�1) = (�1)³ + 3(�1)² � 9(�1) � 20 = �9 Jadi titiknya (�1, �9)
Gambar grafiknya :

Share this post